Courir sous la pluie ?

[pep3000]

Bonjour à tous. Voici un exercice que mon prof de physique m'avait proposé, et que j'ai trouvé amusant :
Imaginez un homme en kawé marchant sous la pluie. On suppose que la pluie tombe verticalement, et que les gouttes tombent à la vitesse u. L'homme a une capuche imperméable, donc il n'est pas mouillé par les gouttes qui tombent SUR sa tête : quand l'homme est à l'arrêt, il n'est pas mouillé. Mais la capuche ne protège pas son visage. Ainsi, quand l'homme avance, il entre en contact avec les gouttes, et son visage se mouille.
L'homme doit parcourir une distance L. Pour être le moins mouillé, à quelle vitesse v doit-il aller ?

J’espère que j'ai réussi a faire un énoncé clair. Si ca n'est pas le cas, dites le moi, j'essayerai de le reformuler.

[ecolami]

Bonjour,
Ainsi présenté je dirai que plus l'homme va vite plus il est mouillé. On n'a abordé qu'une partie du problème puisqu'en avançant il expose les jambes à la pluie: au repos on peut estimer que le kawé protège "bien" les jambes.
(j'ai toujours trouvé qu'il manquait une gouttière au kawé pour éloigner l'eau de ruissellement )

[coton]

Je ne serais pas répondre à ta question, mais pour les curieux, les Mythbusters avaient réalisé un épisode sur ce sujet:
"Courir sous la pluie est-il plus efficace que marcher pour rester sec ? " Saison 1, épisode 1

La vidéo doit pouvoir se trouver sur internet.

[wqsde]

Bonjour
Je ne pense pas que ce soit calculable, vu que l'on n'a pas la surface exposée à la pluie, et on n'a pas non plus la densité de la pluie.

[pep3000]

Ca n'est pas parce que je ne les définies pas dans l'énoncé que l'on ne peut pas s'en servir

[darrigan]

Il ne peut pas utiliser un parapluie comme tout le monde ? c'est vraiment un exercice de physique de math spé ça...

Bon, sinon, as-tu pensé que lorsqu'on court, le corps doit compenser sa vitesse en se penchant vers l'avant ? Le centre de gravité est en avant du corps. Ceci contribue à diminuer l'effet de mouillage du visage !

[pep3000]

Oui c'est vrai qu'en courant on doit se pencher et cela réduira le mouillage du visage. Mais bien sûr tous ces paramètres ne sont pas à prendre en compte pour la résolution de l'exercice. Et si on voulait vraiment être jusqu'au-boutiste, il faudrait prendre en compte la transpiration qui résulte de la course

En prépa j'ai vu des exercices largement pire que celui-ci : je me souviens d'un exercice de thermodynamique "En supposant que les humains sont sphériques et qu'ils ont tous le même apport énergétique journalier, peut-on dire que les hommes des pays froids sont plus grands que ceux des pays chauds ?" . Comme ca, ca à l'air impossible mais en fait une fois qu'on traduit l'énoncé en équation c'est assez facile.

[wqsde]

Et tu as la réponse ?

[chatelot16]

plus il court vite moins il restera longtemps sous la pluie

même raisonnement en voiture ... en france il y a XX accident par heure ... plus on roule vite moins on reste longtemps sur la route , moins on a de chance d'avoir un accident !

plus serieusement si la quantité d'eau qu'on prend dans la figure est une histoire de sinus de l'angle ... au petit angle c'est tout simplement proportionnele a la vitesse ... si on va 2 fois plus vite on prend l'eau 2 fois plus mais ça dure 2 fois moins longtemps ... conclusion meme quantité d'eau dans la figure quel que soit la vitesse

mais plutot que de faire le ce calcul stupide il suffit de pencher la tete en avant !

[wqsde]

si la quantité d'eau qu'on prend dans la figure est une histoire de sinus de l'angle

De quel angle ?

[ecolami]

même raisonnement en voiture ... en france il y a XX accident par heure ... plus on roule vite moins on reste longtemps sur la route , moins on a de chance d'avoir un accident !

Bonsoir,
Je me permet une remarque sur le sujet "accidents & voitures" plus on fait de kilomètres plus on a d'accidents et plus on consomme de carburant. Aprés avoir enfoncé ces portes ouvertes il n'y a plus qu'à se dire qu'en supprimant un maximum de sens interdit on gagnerai sur les 2 tableaux et tout ça sans avoir rien changé ni aux voitures, ni à la façon de conduire des gens. (et encore je n'ai rien dit sur l'usure des voitures et leur taux de renouvellement, la balance commerciale de la France et la pollution associée à la consommation de carburant)
C'est une observation qui me tient à coeur et qui ne rencontre jamais aucun écho! La seule chose que savent dire les ecolo est de ne plus employer la voiture ou de rouler moins mais jamais personne n'évoque cette solution.

[darrigan]

Voici mon raisonnement :

Plaçons-nous dans le repère fixe de la personne. La composante verticale de la vitesse de la pluie reste égale à u. Sa composante horizontale devient égale à v. La vitesse de la pluie est donc u+v (en vecteur), dirigé vers le visage.

A vu d'oeil, le visage est d'autant plus exposé que v/u est grand, mais il faut trouver quelle est la relation mathématique traduisant ceci. Je suppose que c'est comme un flux de vecteur à travers une surface, ce serait le sinus de l'angle A que fait la pluie avec le visage qui entre en compte. Or, sin A = v/h où h est l'hypothénuse du triangle rectangle que forment les deux composantes du vecteur vitesse. h est donc la norme de la vitesse soit
$ h=\sqrt{u^2+v^2} $.
On a donc
$ \sin A=\frac{v}{\sqrt{u^2+v^2}} $

Le temps de parcours de la personne, sur la distance L, est égale à L/v et ce temps va multiplier l'exposition du visage à la pluie. On a donc une exposition totale :
$ E = \sin A \times \frac{L}{v}=\frac{L}{\sqrt{u^2+v^2}} $

Il faut que cette exposition soit minimale en fonction de la vitesse v de la personne :
$ \frac{dE}{dv}=0=\frac{d}{dv}(\frac{L}{\sqrt{u^2+v^2}}) $
$ =-L\frac{v}{(u^2+v^2)^{\frac{3}{2}}} $
Pour des valeurs de L et de u fixées :
- Ceci est égal à 0 quand v=0 (trivial).
- Et cela tend vers 0 quand v devient très grand devant u.

Ma conclusion : Soit courrir bien plus vite que la vitesse de la pluie, soit ne pas bouger.

Pep3000, tu me diras si j'ai juste ?

[Milamber]

Je me souviens avoir lu un article sur le sujet dans Science et Vie Junior il y a de ça... Disons dans les 10-15 ans... (en revanche, pas foutu de me souvenir de la conclusion )
Si des âmes charitables et courageuses sont prêtes a fouiller dans leurs archives.

[wqsde]

Voici mon raisonnement :

Plaçons-nous dans le repère fixe de la personne. La composante verticale de la vitesse de la pluie reste égale à u. Sa composante horizontale devient égale à v. La vitesse de la pluie est donc u+v (en vecteur), dirigé vers le visage.

A vu d'oeil, le visage est d'autant plus exposé que v/u est grand, mais il faut trouver quelle est la relation mathématique traduisant ceci. Je suppose que c'est comme un flux de vecteur à travers une surface, ce serait le sinus de l'angle A que fait la pluie avec le visage qui entre en compte. Or, sin A = v/h où h est l'hypothénuse du triangle rectangle que forment les deux composantes du vecteur vitesse. h est donc la norme de la vitesse soit
$ h=\sqrt{u^2+v^2} $.
On a donc
$ \sin A=\frac{v}{\sqrt{u^2+v^2}} $

Le temps de parcours de la personne, sur la distance L, est égale à L/v et ce temps va multiplier l'exposition du visage à la pluie. On a donc une exposition totale :
$ E = \sin A \times \frac{L}{v}=\frac{L}{\sqrt{u^2+v^2}} $

Il faut que cette exposition soit minimale en fonction de la vitesse v de la personne :
$ \frac{dE}{dv}=0=\frac{d}{dv}(\frac{L}{\sqrt{u^2+v^2}}) $
$ =-L\frac{v}{(u^2+v^2)^{\frac{3}{2}}} $
Pour des valeurs de L et de u fixées :
- Ceci est égal à 0 quand v=0 (trivial).
- Et cela tend vers 0 quand v devient très grand devant u.

Ma conclusion : Soit courrir bien plus vite que la vitesse de la pluie, soit ne pas bouger

[darrigan]

Houla !! attend avant de dire bravo ! Je ne suis moi-même pas convaincu par ma démonstration !

[ecolami]

Bonjour,
Il y des années j'avais déjà lu ce problème et la solution était qu'il fallait courir à une vitesse "infinie" .
Ce qui revenait surtout à dire que moins longtemps on était exposé à la pluie moins on en recevait.
Je ne suis pas sûr mais je crois qu'il existe une vitesse ou la surface du visage reçoit un maximum de pluie et au delà ça diminue.

[pep3000]

Salut à tous !
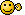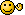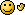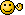
Malgré une démonstration succinte, je pense que c'est Chatelot16 qui a trouvé la bonne réponse, c'est à dire que la vitesse ne change rien. Pour vous en convaincre, je vais essayer de le montrer de deux manières différentes : la première est "statistique" et la deuxième s'appuie sur le raisonnement de Darrigan.

Avant toute chose, je définis le "mouillage", noté M, et égal au nombre de goutte d'eau qui ont touché le visage.

1ere méthode :
On définit la densité moyenne de goutte d'eau, n, en nb de gouttes d'eau par unité de volume. On suppose que les gouttes sont fixes et que c'est l'homme qui avance à la vitesse v. On se fiche donc de la vitesse des gouttes, car on suppose que statistiquement, elles sont perpétuellement remplacées.
Pendant un temps élémentaire dt, le nombre de gouttes d'eau qui ont traversé le visage de surface S, peut s'ecrire comme un flux à travers une surface :
$ dM = \iint\limits_S \,n*\vec{v}\ * \vec{dS}\ * dt = n*v*S*dt $

( $ \vec{dS} $ est le vecteur surface élémentaire, orthogonal par rapport au visage)

(intuitivement : pendant dt, le visage a parcouru la distance $ v*dt $ En multipliant par $ S $, on obtient le volume du pavé droit qui définit le volume "coupé" par le visage de l'homme. Il reste à multiplié par n, et on obtient le nombre de goutte qui ont traversé le visage de l'homme.)

On sait que l'homme va marcher pendant une durée $ T=\frac{L}{v} $. A la fin de sa marche, on a donc :
$ M=\int^T_0 dM = \left[n*v*S*t \right]_0^T = n*v*S*\frac{L}{v} = n*S*L $

(intuitivement : S*L définit le pavé droit qui définit le volume "coupé" par le visage de l'homme. Il reste à multiplié par n, et on obtient le nombre de goutte qui ont traversé le visage de l'homme.)

On voit donc que M est indépendant de la vitesse !

2ème méthode :
La démonstration commence comme celle de Darrigan :
Plaçons-nous dans le repère fixe de la personne. La composante verticale de la vitesse de la pluie reste égale à u. Sa composante horizontale devient égale à v. La vitesse de la pluie est donc $ \vec{h}=\vec{u}+\vec{v} $, dirigé vers le visage.
On peut définir un vecteur densité de pluie : $ \vec{p} = n*\vec{h} $ (qui correspond par exemple à $ \vec{j} $ le vecteur densité de courant pour I)
Alors, pendant une durée dt :
$ dM = \iint\limits_S \,\vec{p}\ * \vec{dS}\ * dt = \iint\limits_S \,n*(\vec{u}+\vec{v}) * \vec{dS}\ * dt = \iint\limits_S \,n*\vec{v} * \vec{dS}\ * dt = n*v*S*dt $ on trouve la même chose que tout à l'heure.

Par rapport à la démonstration de Darrigan, le $ sin(A) $ intervient dans mon produit scalaire $ \vec{p}\ * \vec{dS} $, et le $ \frac{L}{v} $ apparaîtra à l'integration entre 0 et T. Selon moi, le seule problème est que tu ne prend pas en compte la densité de goutte.
Intuitivement, la formule $ M=\frac{L}{\sqrt{u^2+v^2}} $ pose un problème : s'il tombe quelques gouttes à une vitesse lente, on sera plus mouillé que s'il tombe un déluge à une vitesse rapide.

J'espère que ma démonstration est claire. Si vous avez des questions ou des objections n'hésitez pas, je ne prétend pas détenir LA solution

[alexchimiste]

Y'a vraiment que des physiciens pour être en extase devant une telle question et un tel raisonnement

[ecolami]

Pour être le moins mouillé, à quelle vitesse v doit-il aller .

Bonjour,
En relisant cette phrase on se dit qu'il ne faut pas traiter le problème comme s'il s'agissait d'écoper ou de recueillir de l'eau.
Soit le visage est sec soit il est mouillé.
Intuitivement en avançant plus vite on heurtera davantage de gouttes, mais une fois que toute la surface est mouillée il est évident que la vitesse n'aura plus d'influence.

[ecolami]

Bonjour,
Voici une réponse Yahoo! http://fr.news.yahoo.com/faut-courir-%2 ... 35378.html