Dans le jeu Minecraft, l'espace est divisé en blocs élémentaires de différentes natures (terre, air, eau, pierre, quartz, etc) et l'agriculture n'échappe à la règle. Lorsqu'on plante une graine (blé, carotte, pomme de terre...), elle grandit en passant par différents stades :

Figure 1 : illustrations des différents stades de croissance pour le blé, les carottes et les pommes de terre dans le jeu
En appelant $B_n$ le nombre de plantes au stade $n$ de croissance, on peut considérer que ce sont des réactions successives avec des lois de vitesse d'ordre 1 pour les passages $\left \{ n \right \} \rightarrow \left \{ n + 1\right \}$ : $$v_n = k_n \, B_n \; , \, n \in [\![ 0 ; 6 ]\!]$$
et les équations cinétiques associées : $$\frac{\text{d} \, B_0 (t)}{\text{d} t} = - k_0 \; B_0(t) \\
\frac{\text{d} \, B_n (t)}{\text{d} t} = k_{n-1} \; B_{n-1}(t) - k_n \; B_n(t) , \; n \in [\![ 1 ; 6 ]\!] \\
\frac{\text{d} \, B_7 (t)}{\text{d} t} = k_6 \; B_6(t)$$ Et on remarque que le modèle marche bien, on peut mesurer par exemple $B_0$ toutes les minutes et calculer $k_0$ avec une régression linéaire :
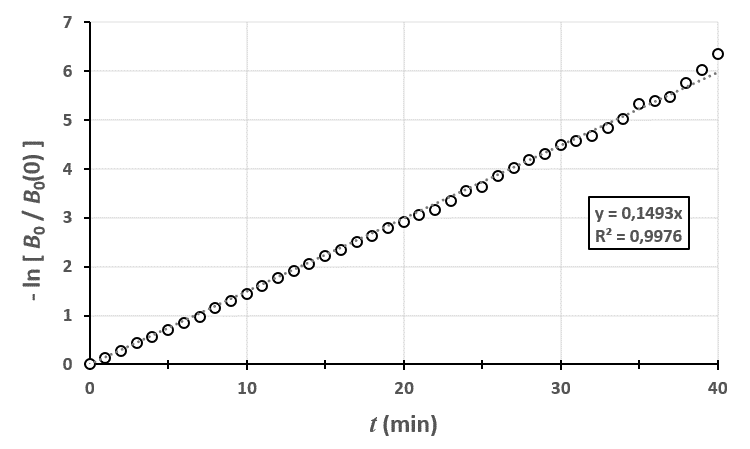
Figure 2 : régression linéaire sur le nombre de plantes au stade 0 au cours du temps
On peut mesurer chacune des 7 constantes de vitesse $k_n$ et vérifier qu'elles sont égales, d'où finalement les solutions :$$B_n(t)=\dfrac{(k_0 \, t)^n}{n \, !} B_0(t) = \dfrac{(k_0 \, t)^n}{n \, !} N \exp(- k_0 \, t) \; , \, n \in \left \{ 0 \, ; \, \cdots \, ; \, 6 \right \} \\
B_7(t) = N - \sum_{n=0}^6 B_n(t) = N \left [ 1 - \sum_{n=0}^6 \dfrac{(k_0 \, t)^n}{n \, !} \exp(- k_0 \, t) \right ] $$ où $N$ est le nombre total de plantes dans le champ (toutes étant au stade 0 au départ de l'expérience).
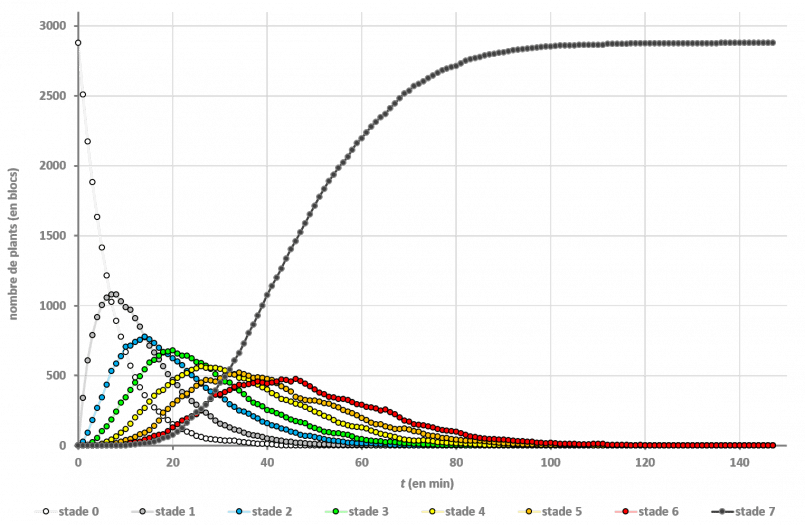
Figure 3 : population des différents stades au cours du temps et superposition avec les modèles numériques.
Mon article complet sur le sujet est ici. Pour une fois que mes cours de chimie peuvent servir dans un jeu vidéo...